The contradiction with Carnotís principle is analyzed. †
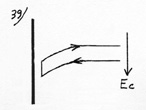
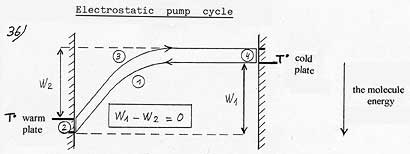
The absence of necessary work to deliver in the process can be easily explained by the fact that each molecule is accelerated† when it arrives on the plate, then slowed down with the same value of energy when it bounces back. W1- W2 = 0. The electric field doesnít provide the molecules withenergy that it cannot recover. The energy is continually given and recovered from the gas molecules when they go to and fro between the plates.
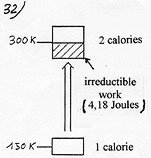
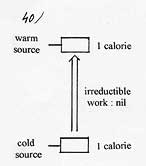
The advantages of this invention are those of the thermoelectric pumps: compactness, simplicity, no parts in motion, so no noise, and adding to this, a very good coefficient of performance able to save energy and reduce pollution ( Efficiency coefficient or coefficient of performance or COP = ratio of the quantity of energy rejected at the warm source (in calories) by the work delivered at the pump (in Joules. 1 calorie = 4.18 joules) ). See also in the applications, the new possibilities induced by this coefficient of performance.
Why can the coefficient of performance of this process go beyond Carnotís ? Comparison of The thermodynamic cycles.
Carnotís theorem :
Q2
(heat rejected at the warm source)† ††=† T2
(temperature of the warm source)
Q1 (heat taken
at the cold source) †††
T1 (temperature of the cold source)
†††††††††††††††††††
|
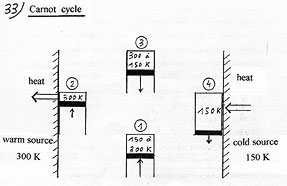
According†† to Carnotís theorem, if one disposes of a cold source, at 150 Kelvin and a warm source at 300 K ( T warm source / T cold source = 2) and takes off† one calorie at the cold source, it induces a minimum rejection of 2 calories at the warm source, the second calorie coming from the minimum work delivered at the pump ( 4.18 joules). In that case, Carnotís COP = 2. To †enlighten the cause of the irreducible work to deliver in all the actual processes, it is necessary to closely observe Carnotís cycle which is a perfect method as far as the minimum amount of work to deliver in a mechanical compression heat pump is concerned. |
Letís consider a mole of perfect gas at 150K
|
|
(1) Adiabatic compression of the gas to reach the temperature of the warm source. (2) After having been put in contact with the warm source, it is compressed again in an isothermal way†† to pour heat into it. This operation must be done very slowly not to overheat the gas compared to the warm source. (3) Adiabatic expansion of the gas to cool it until it reaches the temperature of the cold source. (4) After having been put in contact with the cold source, it is expanded again in an isothermal way ( very slowly ) to draw heat from it. |
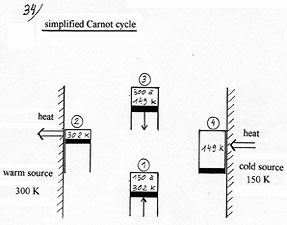
We realize that we reach about the same result by suppressing the compression and the isothermal expansion and by replacing them by a slight difference in temperature between the gas and the cold or warm source when they are put in contact. This method brings us nearer from the thermodynamic cycle of the invention and is going to show clearly the difference and originality of the invention.
|
|
(1)
Adiabatic compression of the gas (1 mole) and warming up from 150
to 302 K (302 K is arbitrarily chosen). (2)
Cooling of the gas after the contact with the warm source, from 302
to 300K. (3)
Adiabatic expansion of the gas and down
from 300 to 149.0066K (4) Warming up of the gas in contact with the cold source from 149.0066K to 150K. Heat received: 12.39 Joules. |
One can sum up the situation with the energetic cycle represented below: If one takes 12.39 Joules at the cold source, 29.94 Joules are rejected at the warm source, that is to say a difference of 12.55 J which corresponds exactly to the work globally spent in the cycle †(w1-w2).
As foreseen, 1 calorie taken at the cold source induces the rejection of 2 calories at the warm source ( 24.94/12.39=2.013). The second calorie coming from the work delivered.
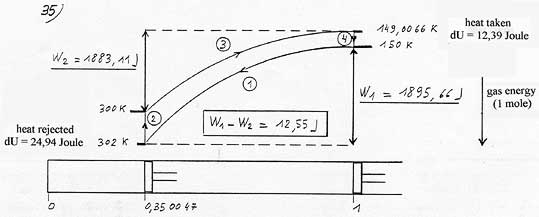
One can see that the gas energy, that is to say its temperature, is on average higher during the compression than during the expansion, simply because it is warmed up just before the compression stage and cooled down just before the expansion stage. Yet, if the gas is warmer during the compression, its pressure is also higher. Consequently the compression work W1 is inevitably more important than the expansion work W2, hence a global irreducible work to deliver. ( i.e.: 12.55J).
|
(1) Acceleration or warming up of the gas molecule in the attraction field. (2) Cooling by thermal accommodation. (3) Slowing down or cooling of the molecule in the attraction field. (4) Warming up by thermal accommodation. |
The work of the piston in Carnot cycle is replaced here by the work of the attraction field and the contact with the cold or warm source in Carnot cycle is done here by thermal accommodation. But, while in Carnot cycle the necessary compression work to warm up the gas (w1) was superior to the expansion work (w2) which was cooling it down, this time the attraction field accelerates then slows down the molecule according to the same potential energy. W1 Ė W2= 0
|
|
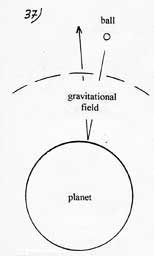
To enlighten this angle, one could compare the molecule which falls on the plate to a ball in space which falls on a planet ( one must assume that there is no atmosphere and that the ball has a very high initial speed). When it penetrates into the gravitational field of the planet, the ball is accelerated. Because of the shock, it yields energy in the shape of heat and so rebounds at a lower speed. When it goes up again, it slows down and goes back into space with a kinetic energy lower than the one it had before falling on the planet. Its energetic curve would exactly corresponds to the one described in the one described in the left part of the diagram above. |
Once out of the gravitational field, the ball has no energetic debt owed to the gravitational field. The later accelerates the ball when it falls down but it slows down as much when it goes up again. The principle of conservation of energy is respected. The energy freed during the shock is paid by a final slowing down of the ball but absolutely not by the gravitational field. It is the same for a molecule in the electrostatic attraction field.
|
|
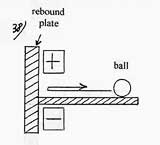
One can be persuaded of it by observing the experiment of the blade which is introduced in the condenser. To have a more vivid imagery, we can replace the blade by a ball which would roll on a horizontal plane as represented on the diagram opposite. By penetrating into the electric field of the condenser, the ball accelerates, its kinetic energy increases of a value corresponding to the attraction energy of the ball, it strikes the rebound plate by yielding energy and so goes back at a lower speed, then it slows down when going out ft the electric field of the condenser. During this operation, if the condenser is maintained at a constant charge (and not at a constant potential), there is no loss of electric energy with a perfect electric insulation. It is exactly the same thing for the molecules in this process. It wasnít the same thing in Carnot cycle where the work done by the acceleration of the molecules during the compression could in no case be totally recovered by their deceleration during the expansion, the heat freed at the warm source was partly paid in return by the work of the piston. To conclude: there is no longer necessarily a work to provide† which would be transformed into heat and rejected at the warm source. In the case where the work is nil, each calorie taken at the cold source is rejected at the warm source and nothing more. Weíll see in the applications the consequences induced by this new propriety. |