Explanation of the electrostatic principle.

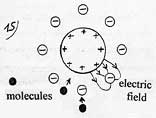
The attraction of molecules by polarization is known in the phenomenon of electrostriction. It is also at the origin of the formation of rare gas hydrates ( Arn H2O). In this example, the argon atoms get polarized and are attracted when close from the water molecule dipole.

The energy of acceleration of a molecule  

penetrating in the electric field is given by:

E pol = ˝ a E2. With a = polarizability of the molecule and E = electric field.

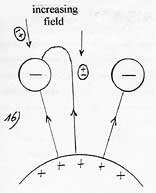
So it is only the average value of the electric field in contact with the electrostatic plate which determines the acceleration energy of the molecules. A grid gives the acceleration energy of a molecule for a few gas and the corresponding heating.

 

Electrostatic principle

Let’s imagine a positively charged metallic bar inside a metal cage connected to the earth, that is to say a Faraday cage. The later neutralizes the electric field out of the cage thanks to the negative charge it carries by influence. If a gas molecule is far from the cage, it doesn’t perceive any electric field and nothing happens. But if it gets close enough from the cage, the screen effect disappears and the molecule gets polarized under the effect of the electric field residing between the bar and the cage (see diagram opposite).

In the case  it penetrates between two bars of the cage, the electrons of the molecule are attracted and its nucleus repelled. But as the electrons are closer from the bar and consequently in a more intense field than in the nucleus, the attraction of the nucleus wins over the repulsion of the electrons. There again, the molecule is attracted. If we take up again the case of a molecule moving on the symmetry axis of a dipole, that is to say perpendicularly to the electric field ( diagram 17), the nucleus of the molecule is attracted towards the negatively charged bar and the electrons towards the positively charged bar, each one of these forces being led tangentially  to the field line. As this line is curved the two opposite attraction forces are thus not parallel. Hence a resultant of forces led towards the increasing field.

The penetration of a molecule into an electric field has always the effect of attracting it towards the increasing field and this having nothing to do with the motion nor the direction of the field. This phenomenon of attraction by electrostatic polarization  of a gas is known under the name of Debye’s force, which is for instance at the origin of the formation of rare gas hydrates ( Arn H2O) with production of heat resulting from the energy of attraction between molecules.

Parameters of the energy of attraction

When a polarizable molecule, such as SF6, penetrates into an electric field, it produces a dipole which induces a difference in absolute value of electric potential energy acquired by both charges, positive and negative. This difference of potential energy is the result of the difference dl between the charges (diagram opposite) caused by the electrostatic force F which separates them at this place.

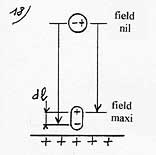
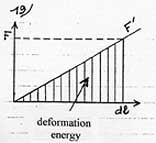
Yet, some of this energy is used to deform the molecule in the same way as energy is needed to set a spring in motion. As the force of deformation F’ varies linearly with dl (diagram 19), the average force of deformation is thus 1/2F, and the energy of deformation 1/2F.dl. Consequently, the remaining energy of 1/2Fdl is the attraction energy of the molecule on the plate. The polarizability of the molecule is

µ = Q.dl/E (en Cm/Vm-1)  So Q.dl = µ.E

On the other hand the electrostatic force which separates the charges

 F = Q.E

so F.dl = Q.E.dl  = µ.E˛

Energy of attraction = ˝ F.dl = ˝ µ.E˛

This formula can be found in different books by different authors.

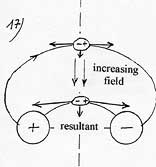
To put it differently the energy of attraction of a polarizable molecule only depends on the value of the electric field at the surface of the plate and this independently of the length of attraction L, that is to say the thickness of the zone of variable field to cross and also independently of the value of the gradient of the electric field. Indeed, for a same electric field of surface, if one doubles the thickness of the zone of variable field, one doubles the length of attraction L but at the same time, one reduces of a half the gradient of the electric field and hence, the gravity. Consequently, the attraction work remains identical.

The grid below gives the attraction energy (or attraction work) and the correspondence in heating degrees for a few examples of gas molecules penetrating in a field of 5 x 108 V/m ( 500 KV/mm) assessing they come from a zone where the field is nil.

The heating of 1°C is equal to about 2.10-23 Joule per molecule of monatomic gas, that is to say 3/2K, with K=1.38 x 10-23 Joule. For a polyatomic molecule such as SF6, the translation energy of the molecule now represents the half of its total energy, the other half being rotation-on-itself energy. To estimate correctly the heating of such a molecule, considering that only the translation energy increases when the molecule penetrates the electric field, one would have to divide by two the heating that one would have if it was a monatomic molecule (which only possesses the translation energy).

Gas

Polarizability
in Cm/Vm-1

Attraction energy
with 5 x 108 V/m

Degrees of heating

Argon
Krypton
Xenon
SF6

1.85 x 10-40
2.96 x 10-40
4.66 x 10-40
7.4 x 10-40

2 x 10-23 Joules
3.2 x 10-23 Joules
5 x 10-23 Joules
8 x 10-23 Joules

1 Kelvin
1.6 K
2.5 K
4/2 K